This module intends to equip students with critical thinking and problem solving skills. It introduces to students on concepts of first and second order both Ordinary and Partial Differential Equations (ODEs & PDEs). In addition it discusses systems of ODEs and Applications of PDEs particular in Physics.
The module introduces students to complex functions and their applications in different disciplines of sciences. It contains the following topics: definition, limits, continuity, differentiation and integration of elementary complex function, Taylor’s and Laurent’s series, Cauchy integral formula, singular points and residue theory, evaluation of definite integrals. It further explores the argument principle and Rouche’s theorem.
1. Welcome message
Dear Students,
I would wish to welcome you in this module MAT3141.
2. Module Aim
The module aims to engage students in a more understanding of the Multivariate
distribution and analysis, Concepts of sampling distribution, Real life applications of
Inferential statistics.
It also introduces to students on practices of what will be covered in theory. After completion
of the module, the student teachers will be able to teach similar topics in secondary schools
and as well as in any other school having a related content.
3. Learning outcomes
Students should be able to:
i. Solve problems involving multivariate distribution and analysis.
ii. Solve problems involving concepts of sampling distribution,
iii. Solve Real life problem requiring knowledge of Inferential statistics.
iv. To perform practices of what will be covered in theory.
4. Facilitators
Jean Francois Maniraho, jmaniraho@ur.ac.rw
Jean Claude Dushimimana, dushimejclau@gmail.com
5. Teaching and Learning Activities
Dear Students, the module is made of units, you will find notes to read before you can
compute for a quiz or assignment, each unit will guide you into this exercise.
For any other question, please do not hesitate to contact the facilitators on the addresses
given above.
This module introduces the student to functions of many variables: Domains of definition, levels lines and surfaces, Limits and continuity; Partial derivatives, Schwartz theorem, chain rule; Total differentiation, directional derivative and gradient; Optimization: critical points given a formula, maxima and minima, second derivative test; Multiple integrals, curvilinear and surface integrals and their applications; Gradient, divergence and curl of vector valued functions and Green and Stokes theorems.
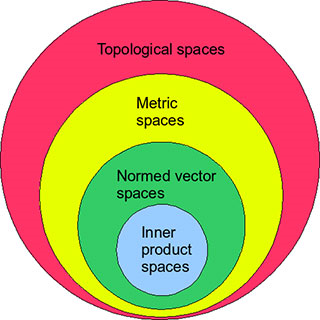
The purpose of this module is to equip students with concepts of general topology such as topological spaces and their properties, mapping between topological spaces, homeomorphism, compactness, connectedness, reparability, It will also explore functional spaces such as Normed vector spaces, Banach, Hilbert, Linear operators, space of generalised functions and Sobolev spaces, Lebesgue integration and Gram–Schmidt orthogonalization in Sobolev spaces.